Publications

Generating Human Interaction Motions in Scenes with Text Control

H. Yi, J. Thies, M.J. Black, X.B. Peng, D. Rempe. arXiv, 2024.

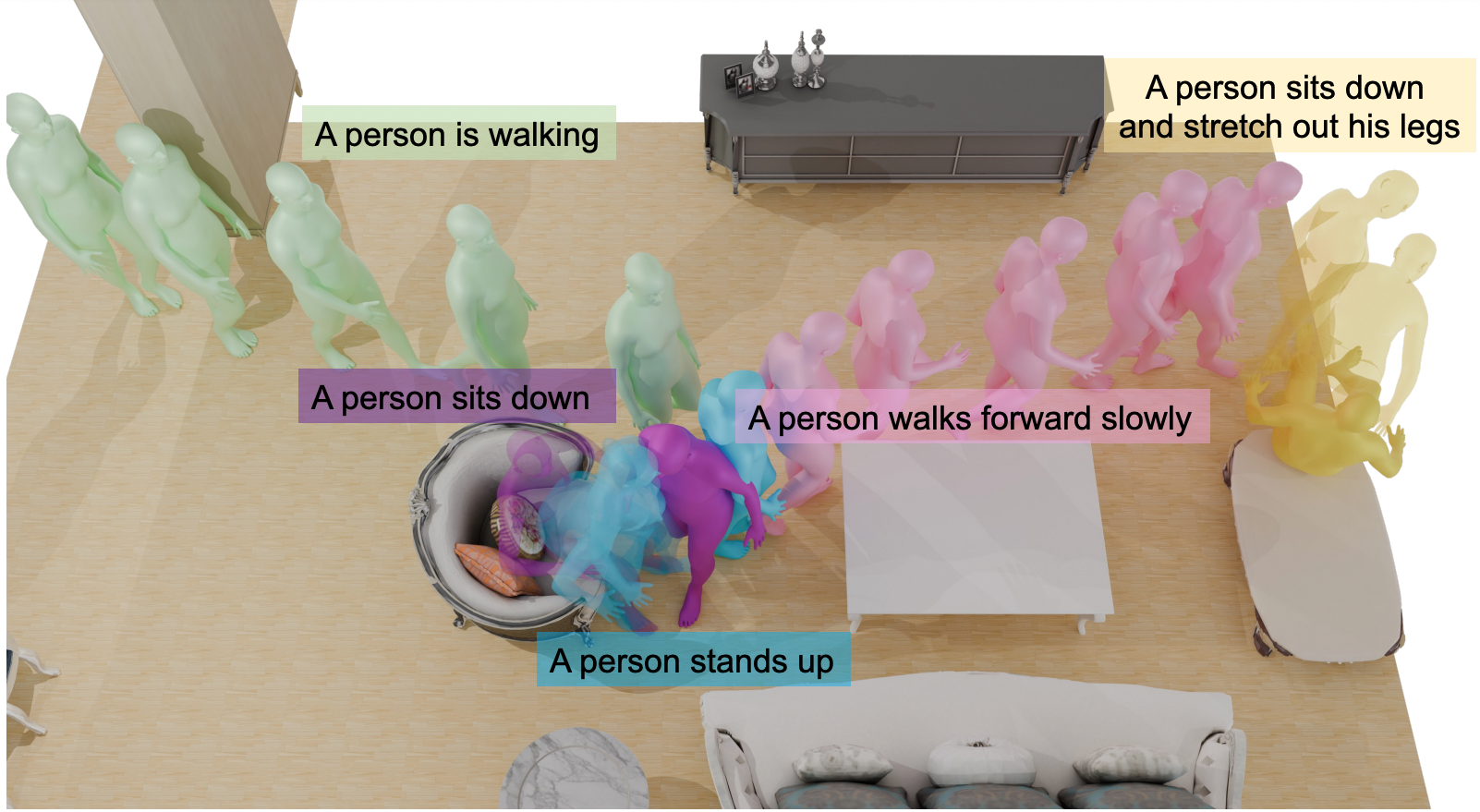
We present TeSMo, a method for text-controlled scene-aware motion generation based on denoising diffusion models. Previous text-to-motion methods focus on characters in isolation without considering scenes due to the limited availability of datasets that include motion, text descriptions, and interactive scenes. Our approach begins with pre-training a scene-agnostic text-to-motion diffusion model, emphasizing goal-reaching constraints on large-scale motion-capture datasets. We then enhance this model with a scene-aware component, fine-tuned using data augmented with detailed scene information, including ground plane and object shapes. To facilitate training, we embed annotated navigation and interaction motions within scenes. The proposed method produces realistic and diverse human-object interactions, such as navigation and sitting, in different scenes with various object shapes, orientations, initial body positions, and poses. Extensive experiments demonstrate that our approach surpasses prior techniques in terms of the plausibility of human-scene interactions, as well as the realism and variety of the generated motions.

Multi-Track Timeline Control for Text-Driven 3D Human Motion Generation

M. Petrovich, O. Litany, U. Iqbal, M.J. Black, G. Varol, X.B. Peng, D. Rempe. CVPR Workshop on Human Motion Generation, 2024.

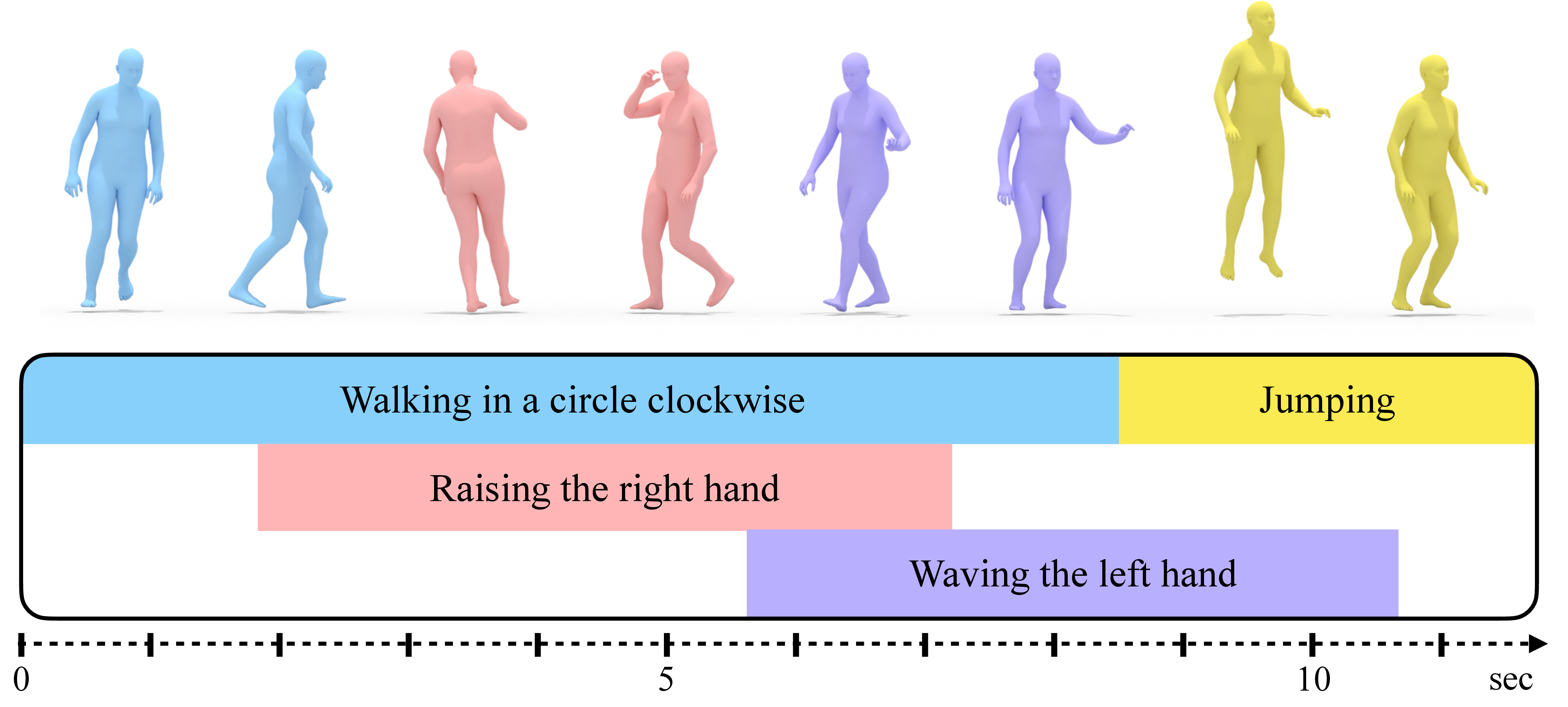
Recent advances in generative modeling have led to promising progress on synthesizing 3D human motion from text, with methods that can generate character animations from short prompts and specified durations. However, using a single text prompt as input lacks the fine-grained control needed by animators, such as composing multiple actions and defining precise durations for parts of the motion. To address this, we introduce the new problem of timeline control for text-driven motion synthesis, which provides an intuitive, yet fine-grained, input interface for users. Instead of a single prompt, users can specify a multi-track timeline of multiple prompts organized in temporal intervals that may overlap. This enables specifying the exact timings of each action and composing multiple actions in sequence or at overlapping intervals. To generate composite animations from a multi-track timeline, we propose a new test-time denoising method. This method can be integrated with any pre-trained motion diffusion model to synthesize realistic motions that accurately reflect the timeline. At every step of denoising, our method processes each timeline interval (text prompt) individually, subsequently aggregating the predictions with consideration for the specific body parts engaged in each action. Experimental comparisons and ablations validate that our method produces realistic motions that respect the semantics and timing of given text prompts.

NIFTY: Neural Object Interaction Fields for Guided Human Motion Synthesis

N. Kulkarni, D. Rempe, K. Genova, A. Kundu, J. Johnson, D. Fouhey, L. Guibas. Conference on Computer Vision and Pattern Recognition (CVPR), 2024.

We address the problem of generating realistic 3D motions of humans interacting with objects in a scene. Our key idea is to create a neural interaction field attached to a specific object, which outputs the distance to the valid interaction manifold given a human pose as input. This interaction field guides the sampling of an object-conditioned human motion diffusion model, so as to encourage plausible contacts and affordance semantics. To support interactions with scarcely available data, we propose an automated synthetic data pipeline. For this, we seed a pre-trained motion model, which has priors for the basics of human movement, with interaction-specific anchor poses extracted from limited motion capture data. Using our guided diffusion model trained on generated synthetic data, we synthesize realistic motions for sitting and lifting with several objects, outperforming alternative approaches in terms of motion quality and successful action completion. We call our framework NIFTY: Neural Interaction Fields for Trajectory sYnthesis.

CurveCloudNet: Processing Point Clouds with 1D Structure

C. Stearns, J. Liu, D. Rempe, D. Paschalidou, J. Park, and L. Guibas. Conference on Computer Vision and Pattern Recognition (CVPR), 2024.

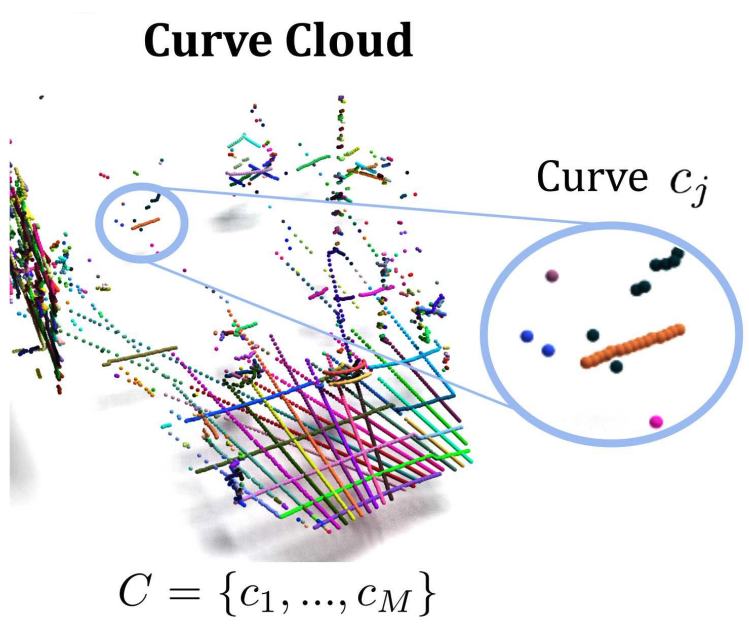
Modern depth sensors such as LiDAR operate by sweeping laser-beams across the scene, resulting in a point cloud with notable 1D curve-like structures. In this work, we introduce a new point cloud processing scheme and backbone, called CurveCloudNet, which takes advantage of the curve-like structure inherent to these sensors. While existing backbones discard the rich 1D traversal patterns and rely on Euclidean operations, CurveCloudNet parameterizes the point cloud as a collection of polylines (dubbed a "curve cloud"), establishing a local surface-aware ordering on the points. Our method applies curve-specific operations to process the curve cloud, including a symmetric 1D convolution, a ball grouping for merging points along curves, and an efficient 1D farthest point sampling algorithm on curves. By combining these curve operations with existing point-based operations, CurveCloudNet is an efficient, scalable, and accurate backbone with low GPU memory requirements. Evaluations on the ShapeNet, Kortx, Audi Driving, and nuScenes datasets demonstrate that CurveCloudNet outperforms both point-based and sparse-voxel backbones in various segmentation settings, notably scaling better to large scenes than point-based alternatives while exhibiting better single object performance than sparse-voxel alternatives.

Language-Guided Traffic Simulation via Scene-Level Diffusion

Z. Zhong, D. Rempe, Y. Chen, B. Ivanovic, Y. Cao, D. Xu, M. Pavone, and B. Ray. Conference on Robot Learning (CoRL), 2023.

Oral Presentation

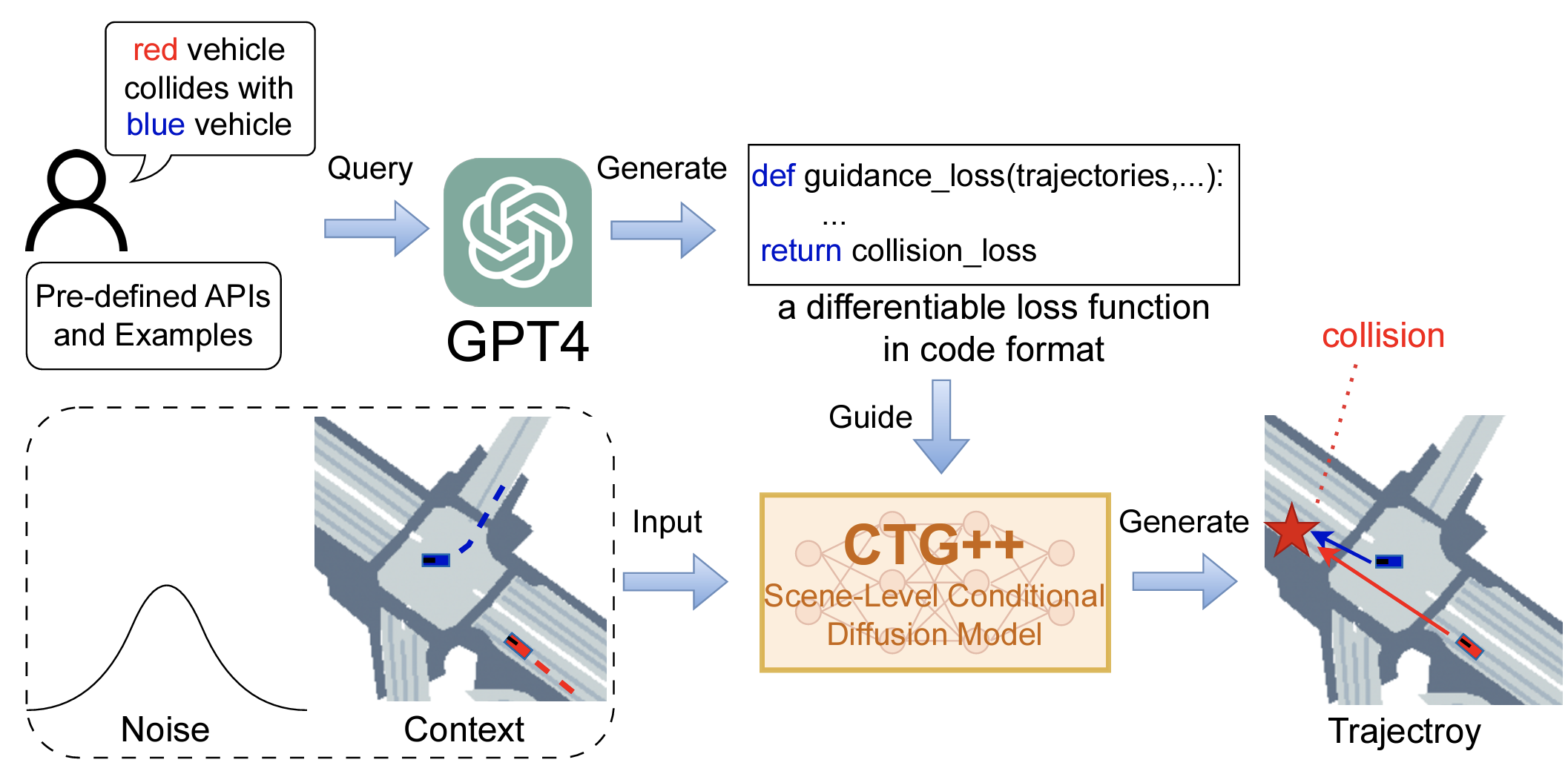
Realistic and controllable traffic simulation is a core capability that is necessary to accelerate autonomous vehicle (AV) development. However, current approaches for controlling learning-based traffic models require significant domain expertise and are difficult for practitioners to use. To remedy this, we present CTG++, a scene-level conditional diffusion model that can be guided by language instructions. Developing this requires tackling two challenges: the need for a realistic and controllable traffic model backbone, and an effective method to interface with a traffic model using language. To address these challenges, we first propose a scene-level diffusion model equipped with a spatio-temporal transformer backbone, which generates realistic and controllable traffic. We then harness a large language model (LLM) to convert a user's query into a loss function, guiding the diffusion model towards query-compliant generation. Through comprehensive evaluation, we demonstrate the effectiveness of our proposed method in generating realistic, query-compliant traffic simulations.

COPILOT: Human-Environment Collision Prediction and Localization from Multi-view Egocentric Videos

B. Pan, B. Shen, D. Rempe, D. Paschalidou, K. Mo, Y. Yang, and L. Guibas. International Conference on Computer Vision (ICCV), 2023.

The ability to forecast human-environment collisions from egocentric observations is vital to enable collision avoidance in applications such as VR, AR, and wearable assistive robotics. In this work, we introduce the challenging problem of predicting collisions in diverse environments from multi-view egocentric videos captured from body-mounted cameras. Solving this problem requires a generalizable perception system that can classify which human body joints will collide and estimate a collision region heatmap to localize collisions in the environment. To achieve this, we propose a transformer-based model called COPILOT to perform collision prediction and localization simultaneously, which accumulates information across multi-view inputs through a novel 4D space-time-viewpoint attention mechanism. To train our model and enable future research on this task, we develop a synthetic data generation framework that produces egocentric videos of virtual humans moving and colliding within diverse 3D environments. This framework is then used to establish a large-scale dataset consisting of 8.6M egocentric RGBD frames. Extensive experiments show that COPILOT generalizes to unseen synthetic as well as real-world scenes. We further demonstrate COPILOT outputs are useful for downstream collision avoidance through simple closed-loop control.

Trace and Pace: Controllable Pedestrian Animation via Guided Trajectory Diffusion

D. Rempe, Z. Luo, X.B. Peng, Y. Yuan, K. Kitani, K. Kreis, S. Fidler, and O. Litany. Conference on Computer Vision and Pattern Recognition (CVPR), 2023.

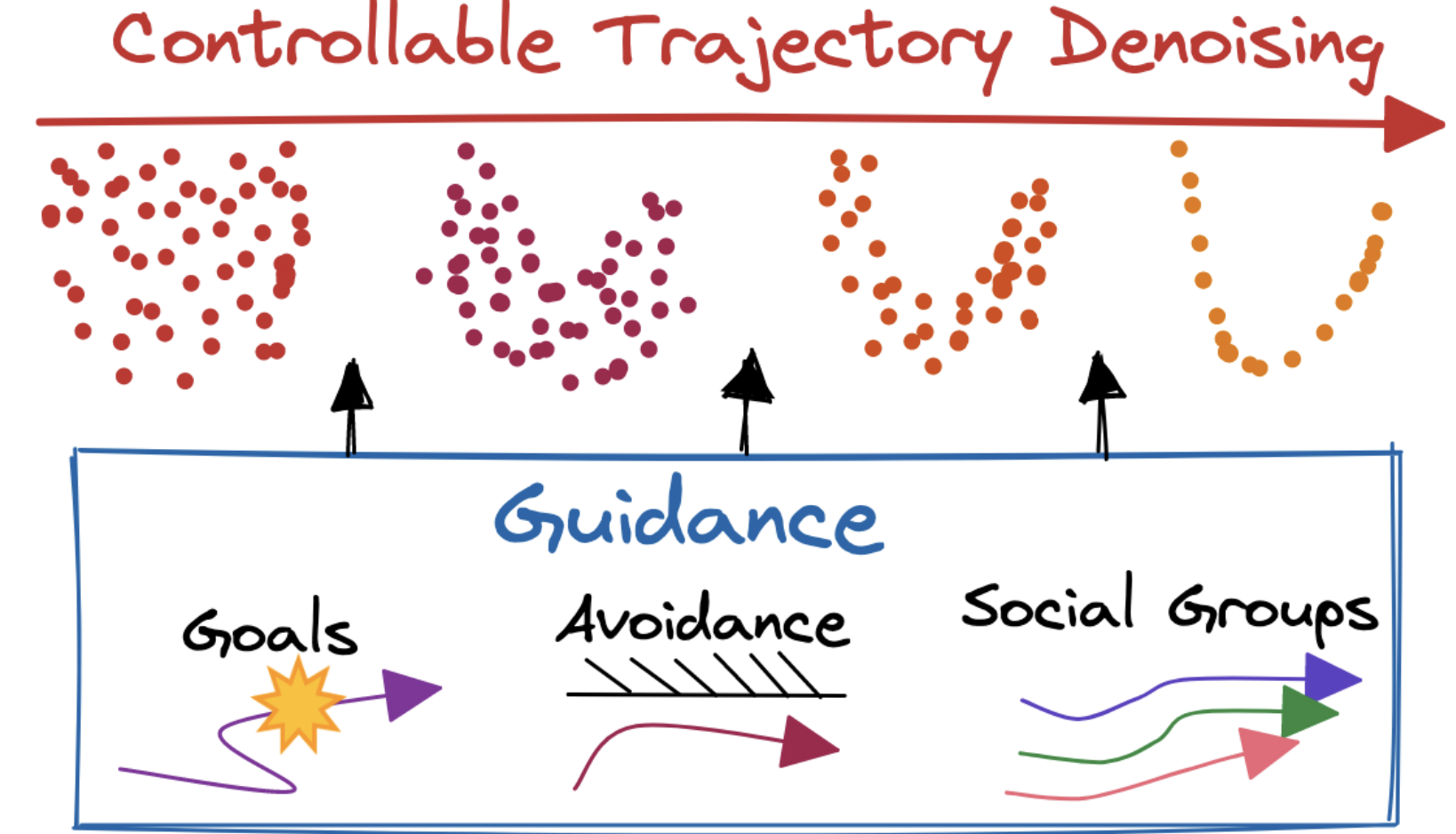
We introduce a method for generating realistic pedestrian trajectories and full-body animations that can be controlled to meet user-defined goals. We draw on recent advances in guided diffusion modeling to achieve test-time controllability of trajectories, which is normally only associated with rule-based systems. Our guided diffusion model allows users to constrain trajectories through target waypoints, speed, and specified social groups while accounting for the surrounding environment context. This trajectory diffusion model is integrated with a novel physics-based humanoid controller to form a closed-loop, full-body pedestrian animation system capable of placing large crowds in a simulated environment with varying terrains. We further propose utilizing the value function learned during RL training of the animation controller to guide diffusion to produce trajectories better suited for particular scenarios such as collision avoidance and traversing uneven terrain.

Guided Conditional Diffusion for Controllable Traffic Simulation

Z. Zhong, D. Rempe, D. Xu, Y. Chen, S. Veer, T. Che, B. Ray, and M. Pavone. International Conference on Robotics and Automation (ICRA), 2023.

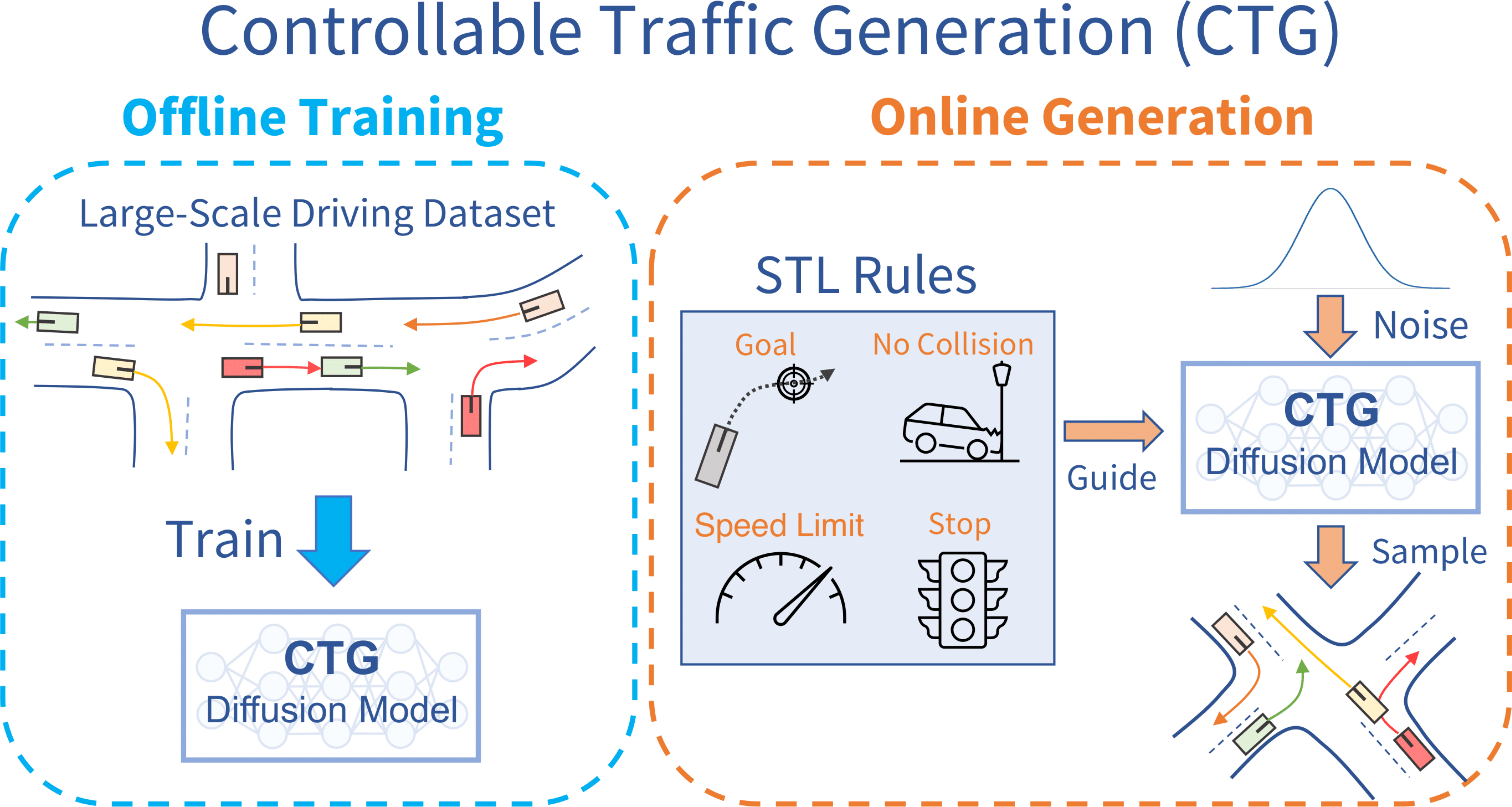
Controllable and realistic traffic simulation is critical for developing and verifying autonomous vehicles. Typical heuristic-based traffic models offer flexible control to make vehicles follow specific trajectories and traffic rules. On the other hand, data-driven approaches generate realistic and human-like behaviors, improving transfer from simulated to real-world traffic. However, to the best of our knowledge, no traffic model offers both controllability and realism. In this work, we develop a conditional diffusion model for controllable traffic generation (CTG) that allows users to control desired properties of trajectories at test time (e.g., reach a goal or follow a speed limit) while maintaining realism and physical feasibility through enforced dynamics. The key technical idea is to leverage recent advances from diffusion modeling and differentiable logic to guide generated trajectories to meet rules defined using signal temporal logic (STL). We further extend guidance to multi-agent settings and enable interaction-based rules like collision avoidance. CTG is extensively evaluated on the nuScenes dataset for diverse and composite rules, demonstrating improvement over strong baselines in terms of the controllability-realism tradeoff.

SpOT: Spatiotemporal Modeling for 3D Object Tracking

C. Stearns, D. Rempe, J. Li, R. Ambrus, S. Zakharov, V. Guizilini, Y. Yang, and L. Guibas. European Conference on Computer Vision (ECCV), 2022.

Oral Presentation

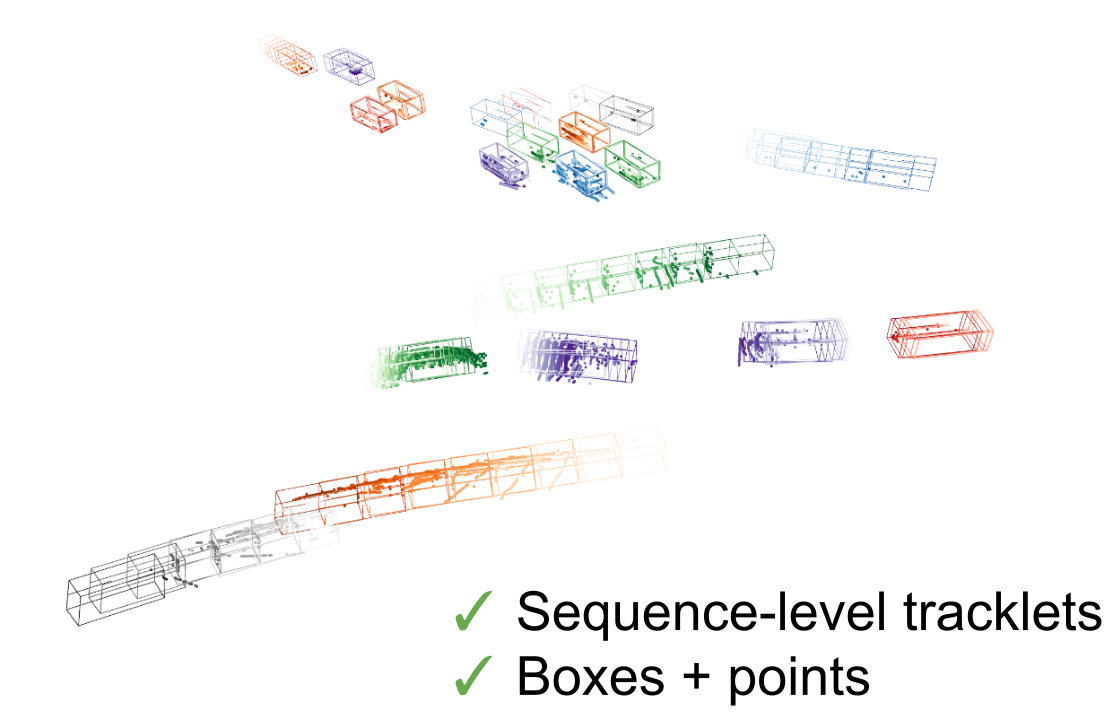
3D multi-object tracking aims to uniquely and consistently identify all mobile entities through time. Despite the rich spatiotem- poral information available in this setting, current 3D tracking meth- ods primarily rely on abstracted information and limited history, e.g. single-frame object bounding boxes. In this work, we develop a holistic representation of traffic scenes that leverages both spatial and tempo- ral information of the actors in the scene. Specifically, we reformulate tracking as a spatiotemporal problem by representing tracked objects as sequences of time-stamped points and bounding boxes over a long tem- poral history. At each timestamp, we improve the location and motion estimates of our tracked objects through learned refinement over the full sequence of object history. By considering time and space jointly, our representation naturally encodes fundamental physical priors such as object permanence and consistency across time. Our spatiotemporal tracking framework achieves state-of-the-art performance on the Waymo and nuScenes benchmarks.

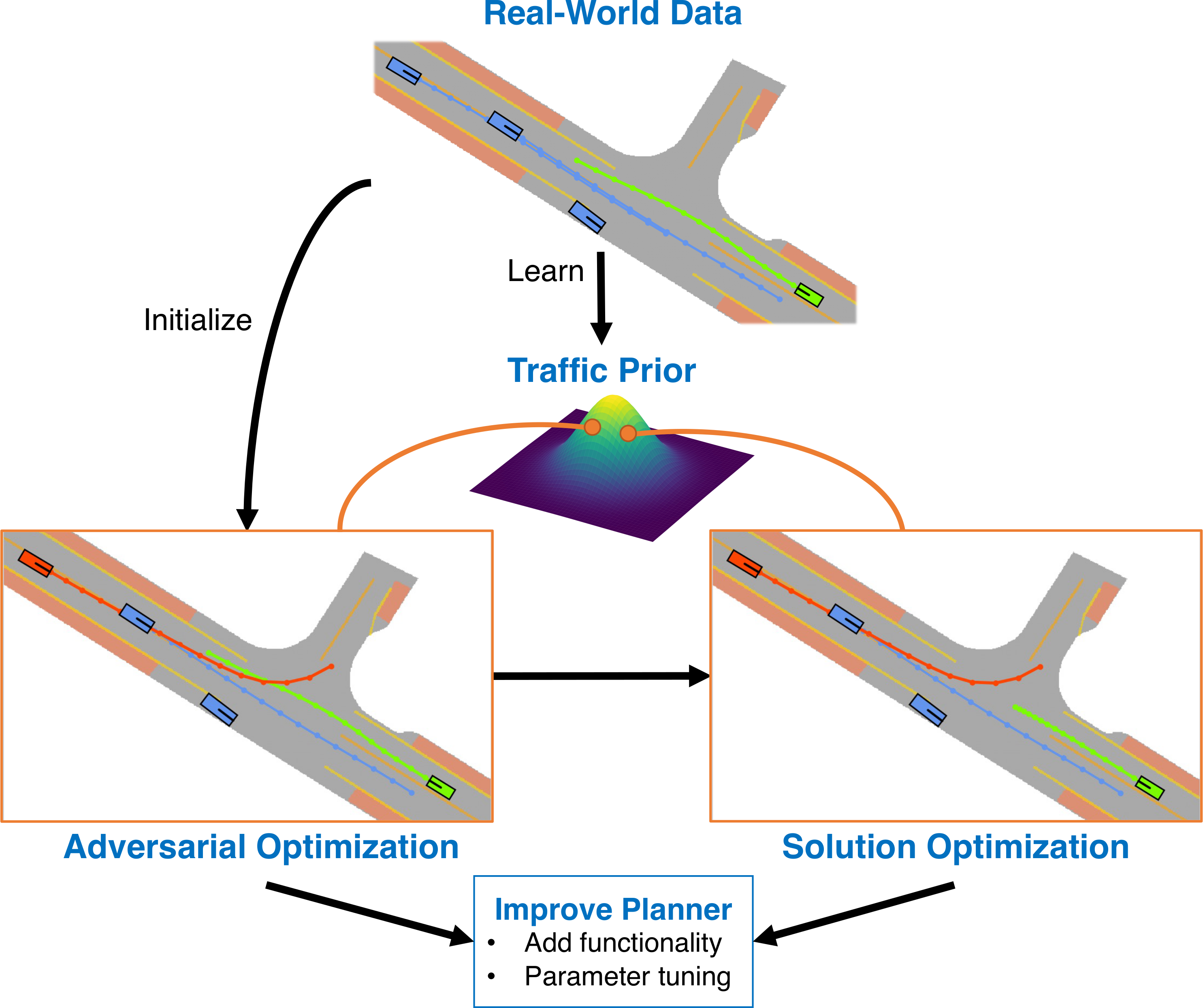
Generating Useful Accident-Prone Driving Scenarios via a Learned Traffic Prior

D. Rempe, J. Philion, L. Guibas, S. Fidler, and O. Litany. Conference on Computer Vision and Pattern Recognition (CVPR), 2022.

Evaluating and improving planning for autonomous vehicles requires scalable generation of long-tail traffic scenarios. To be useful, these scenarios must be realistic and challenging, but not impossible to drive through safely. In this work, we introduce STRIVE, a method to automatically generate challenging scenarios that cause a given planner to produce undesirable behavior, like collisions. To maintain scenario plausibility, the key idea is to leverage a learned model of traffic motion in the form of a graph-based conditional VAE. Scenario generation is formulated as an optimization in the latent space of this traffic model, perturbing an initial real-world scene to produce trajectories that collide with a given planner. A subsequent optimization is used to find a "solution" to the scenario, ensuring it is useful to improve the given planner. Further analysis clusters generated scenarios based on collision type. We attack two planners and show that STRIVE successfully generates realistic, challenging scenarios in both cases. 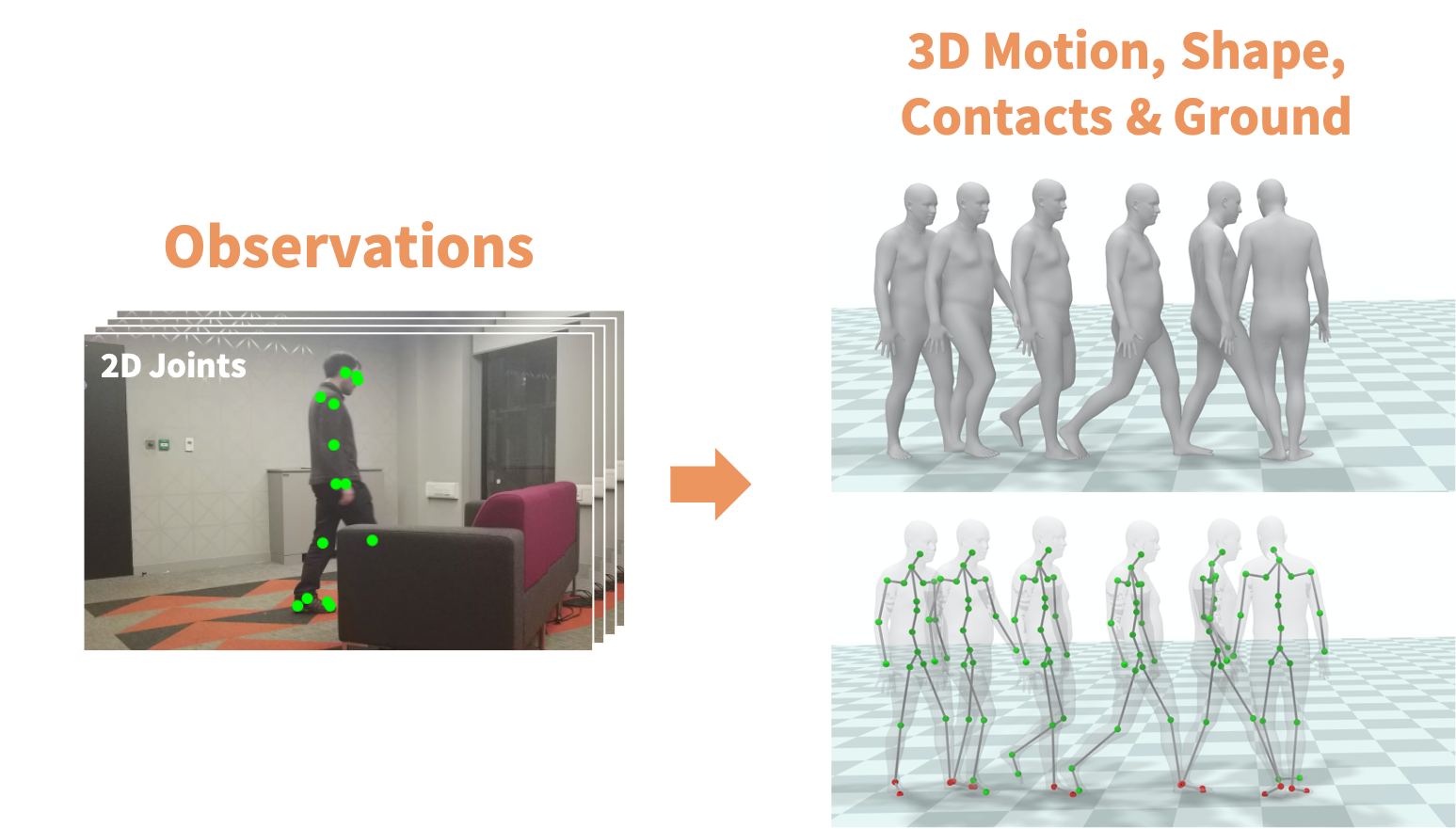We additionally "close the loop" and use these scenarios to optimize hyperparameters of a rule-based planner.

HuMoR: 3D Human Motion Model for Robust Pose Estimation

D. Rempe, T. Birdal, A. Hertzmann, J. Yang, S. Sridhar, and L. Guibas. International Conference on Computer Vision (ICCV), 2021.

Oral Presentation

We introduce HuMoR: a 3D Human Motion Model for Robust Estimation of temporal pose and shape. Though substantial progress has been made in estimating 3D human motion and shape from dynamic observations, recovering plausible pose sequences in the presence of noise and occlusions remains a challenge. For this purpose, we propose an expressive generative model in the form of a conditional variational autoencoder, which learns a distribution of the change in pose at each step of a motion sequence. Furthermore, we introduce a flexible optimization-based approach that leverages HuMoR as a motion prior to robustly estimate plausible pose and shape from ambiguous observations. Through extensive evaluations, we demonstrate that our model generalizes to diverse motions and body shapes after training on a large motion capture dataset, and enables motion reconstruction from multiple input modalities including 3D keypoints and RGB(-D) videos.

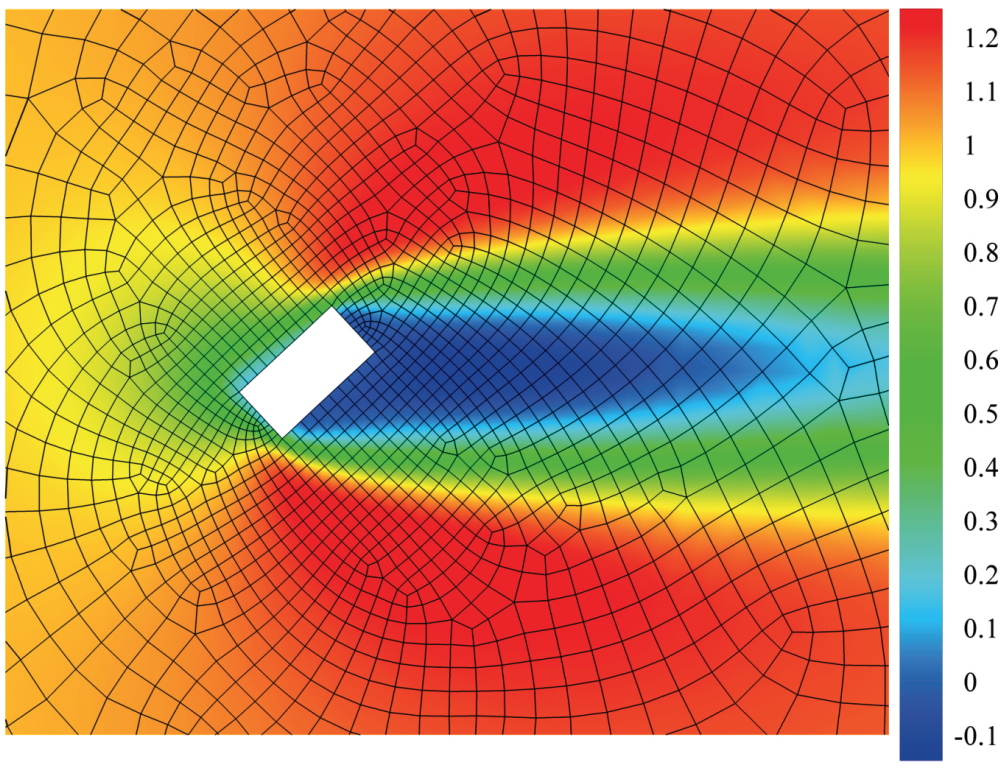
A point-cloud deep learning framework for prediction of fluid flow fields on irregular geometries

A. Kashefi, D. Rempe, and L. Guibas. Physics of Fluids, 2021.

We present a novel deep learning framework for flow field predictions in irregular domains when the solution is a function of the geometry of either the domain or objects inside the domain. Grid vertices in a computational fluid dynamics (CFD) domain are viewed as point clouds and used as inputs to a neural network based on the PointNet architecture, which learns an end-to-end mapping between spatial positions and CFD quantities. Using our approach, (i) the network inherits desirable features of unstructured meshes (e.g., fine and coarse point spacing near the object surface and in the far field, respectively), which minimizes network training cost; (ii) object geometry is accurately represented through vertices located on object boundaries, which maintains boundary smoothness and allows the network to detect small changes between geometries and (iii) no data interpolation is utilized for creating training data; thus accuracy of the CFD data is preserved. None of these features are achievable by extant methods based on projecting scattered CFD data into Cartesian grids and then using regular convolutional neural networks. Incompressible laminar steady flow past a cylinder with various shapes for its cross section is considered. The mass and momentum of predicted fields are conserved. We test the generalizability of our network by predicting the flow around multiple objects as well as an airfoil, even though only single objects and no airfoils are observed during training. The network predicts the flow fields hundreds of times faster than our conventional CFD solver, while maintaining excellent to reasonable accuracy.

CaSPR: Learning Canonical Spatiotemporal Point Cloud Representations

D. Rempe, T. Birdal, Y. Zhao, Z. Gojcic, S. Sridhar, and L. Guibas. Advances in Neural Information Processing Systems (NeurIPS), 2020.

Spotlight Presentation

We propose CaSPR, a method to learn object-centric canonical spatiotemporal point cloud representations of dynamically moving or evolving objects. Our goal is to enable information aggregation over time and the interrogation of object state at any spatiotemporal neighborhood in the past, observed or not. Different from previous work, CaSPR learns representations that support spacetime continuity, are robust to variable and irregularly spacetime-sampled point clouds, and generalize to unseen object instances. Our approach divides the problem into two subtasks. First, we explicitly encode time by mapping an input point cloud sequence to a spatiotemporally-canonicalized object space. We then leverage this canonicalization to learn a spatiotemporal latent representation using neural ordinary differential equations and a generative model of dynamically evolving shapes using continuous normalizing flows. We demonstrate the effectiveness of our method on several applications including shape reconstruction, camera pose estimation, continuous spatiotemporal sequence reconstruction, and correspondence estimation from irregularly or intermittently sampled observations.

Contact and Human Dynamics from Monocular Video

D. Rempe, L. Guibas, A. Hertzmann, B. Russell, R. Villegas, and J. Yang. European Conference on Computer Vision (ECCV), 2020.

Spotlight Presentation

Existing deep models predict 2D and 3D kinematic poses from video that are approximately accurate, but contain visible errors that violate physical constraints, such as feet penetrating the ground and bodies leaning at extreme angles. In this paper, we present a physics-based method for inferring 3D human motion from video sequences that takes initial 2D and 3D pose estimates as input. We first estimate ground contact timings with a novel prediction network which is trained without hand-labeled data. A physics-based trajectory optimization then solves for a physically-plausible motion, based on the inputs. We show this process produces motions that are significantly more realistic than those from purely kinematic methods, substantially improving quantitative measures of both kinematic and dynamic plausibility. We demonstrate our method on character animation and pose estimation tasks on dynamic motions of dancing and sports with complex contact patterns.

Predicting the Physical Dynamics of Unseen 3D Objects

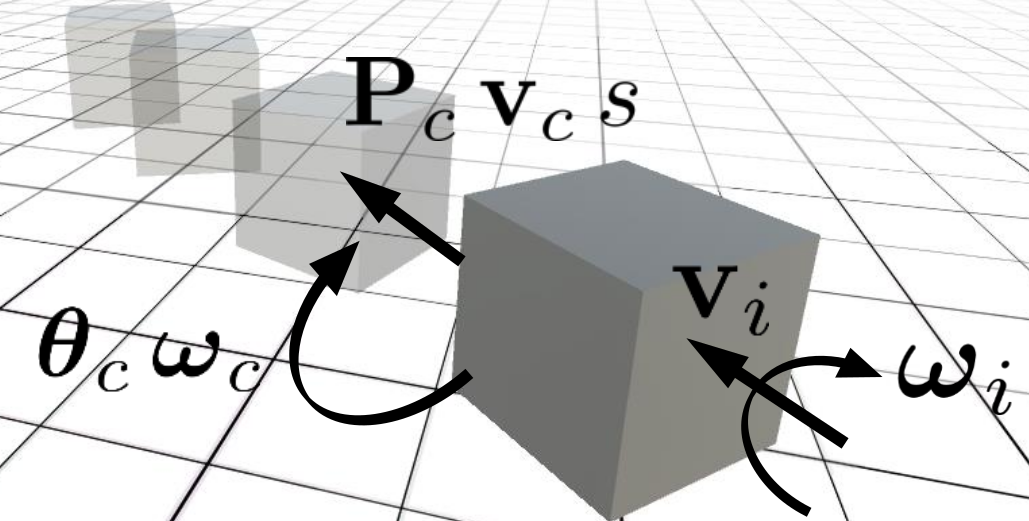
D. Rempe, S. Sridhar, H. Wang, and L. Guibas. Winter Conference on Applications of Computer Vision (WACV), 2020.

Machines that can predict the effect of physical interactions on the dynamics of previously unseen object instances are important for creating better robots, autonomous vehicles, and interactive virtual worlds. In this work, we focus on predicting the dynamics of 3D objects on a plane that have just been subjected to an impulsive force. In particular, we predict the changes in state---3D position, rotation, velocities, and stability. Different from previous work, our approach can generalize dynamics predictions to object shapes and initial conditions that were unseen during training. Our method takes the 3D object's shape as a point cloud and its initial linear and angular velocities as input. We extract shape features and use a recurrent neural network to predict the full change in state at each time step. Our model can support training with data from both a physics engine or the real world. Experiments show that we can accurately predict the changes in state for unseen object geometries and initial conditions.

Multiview Aggregation for Learning Category-Specific Shape Reconstruction

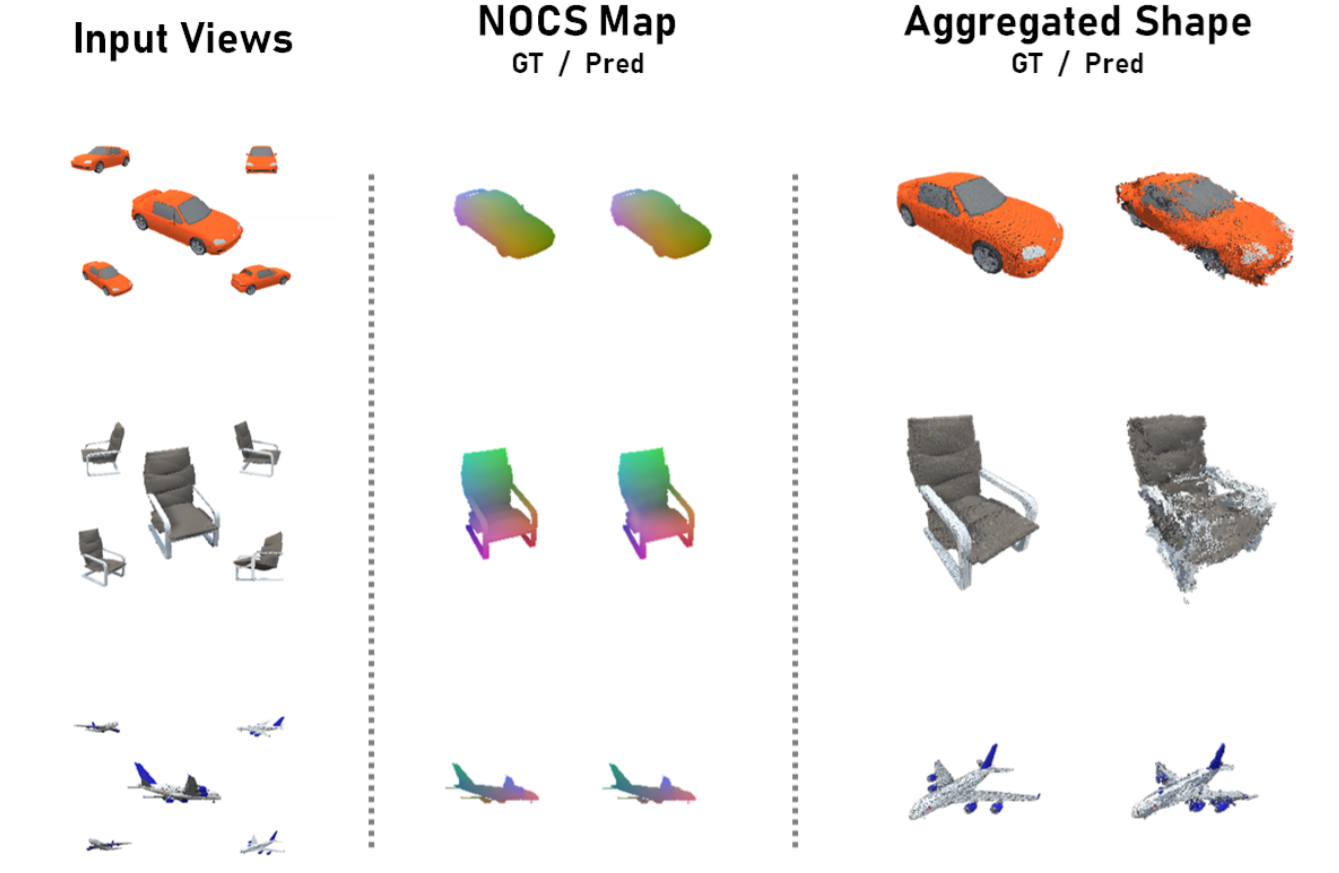
S. Sridhar, D. Rempe, J. Valentin, S. Bouaziz, and L. Guibas. Advances in Neural Information Processing Systems (NeurIPS), 2019.

We investigate the problem of learning category-specific 3D shape reconstruction from a variable number of RGB views of previously unobserved object instances. Most approaches for multiview shape reconstruction operate on sparse shape representations, or assume a fixed number of views. We present a method that can estimate dense 3D shape, and aggregate shape across multiple and varying number of input views. Given a single input view of an object instance, we propose a representation that encodes the dense shape of the visible object surface as well as the surface behind line of sight occluded by the visible surface. When multiple input views are available, the shape representation is designed to be aggregated into a single 3D shape using an inexpensive union operation. We train a 2D CNN to learn to predict this representation from a variable number of views (1 or more). We further aggregate multiview information by using permutation equivariant layers that promote order-agnostic view information exchange at the feature level. Experiments show that our approach is able to produce dense 3D reconstructions of objects that improve in quality as more views are added.

Learning Generalizable Final-State Dynamics of 3D Rigid Objects

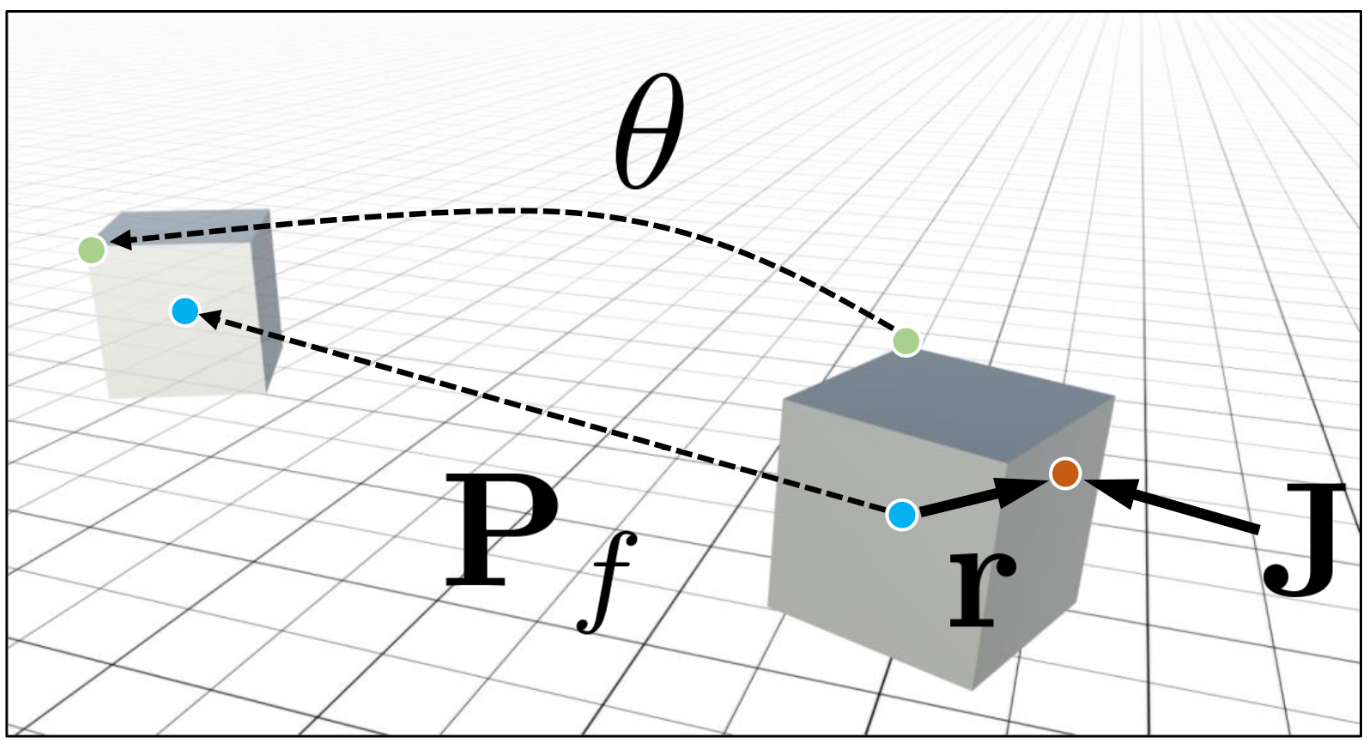
D. Rempe, S. Sridhar, H. Wang, and L. Guibas. CVPR Workshop on 3D Scene Understanding for Vision, Graphics, and Robotics, 2019.

Humans have a remarkable ability to predict the effect of physical interactions on the dynamics of objects. Endowing machines with this ability would allow important applications in areas like robotics and autonomous vehicles. In this work, we focus on predicting the dynamics of 3D rigid objects, in particular an object's final resting position and total rotation when subjected to an impulsive force. Different from previous work, our approach is capable of generalizing to unseen object shapes---an important requirement for real-world applications. To achieve this, we represent object shape as a 3D point cloud that is used as input to a neural network, making our approach agnostic to appearance variation. The design of our network is informed by an understanding of physical laws. We train our model with data from a physics engine that simulates the dynamics of a large number of shapes. Experiments show that we can accurately predict the resting position and total rotation for unseen object geometries.

Effectiveness of Global, Low-Degree Polynomial Transformations for GCxGC Data Alignment

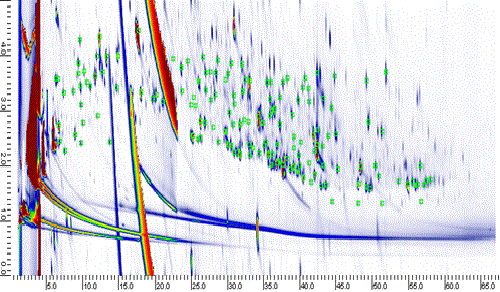
D. Rempe, S. Reichenbach, Q. Tao, C. Cordero, W. Rathbun, and C.A. Zini. Analytical Chemistry, 88(20), pp. 10028-10035, 2016.

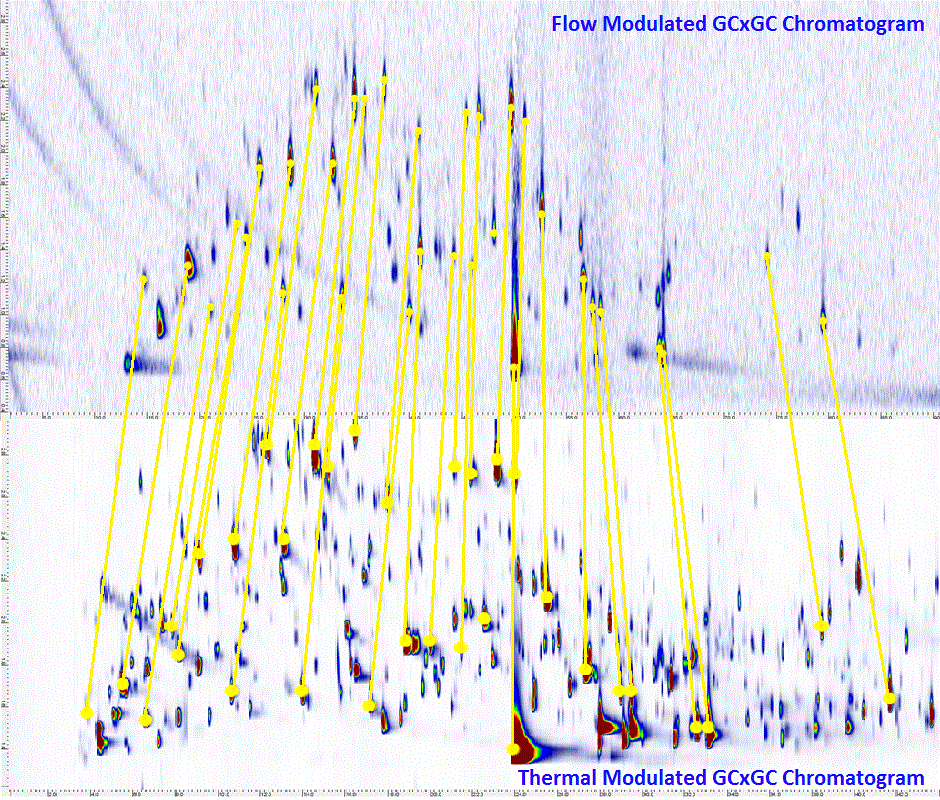
As columns age and differ between systems, retention times for comprehensive two-dimensional gas chromatography (GCxGC) may vary between runs. In order to properly analyze GCxGC chromatograms, it often is desirable to align the retention times of chromatographic features, such as analyte peaks, between chromatograms. Previous work by the authors has shown that global, low-degree polynomial transformation functions – namely affine, second-degree polynomial, and third-degree polynomial – are effective for aligning pairs of two-dimensional chromatograms acquired with dual second columns and detectors (GCx2GC). This work assesses the experimental performance of these global methods on more general GCxGC chromatogram pairs and com- pares their performance to that of a recent, robust, local alignment algorithm for GCxGC data [Gros et al., Anal. Chem. 2012, 84, 9033]. Measuring performance with the root-mean-square (RMS) residual differences in retention times for matched peaks suggests that global, low-degree polynomial transformations outperform the local algorithm given a sufficiently large set of alignment points, and are able to improve misalignment by over 95% based on a lower-bound benchmark of inherent variability. However, with small sets of alignment points, the local method demonstrated lower error rates (although with greater computational overhead). For GCxGC chromatogram pairs with only slight initial misalignment, none of the global or local methods performed well. In some cases with initial misalignment near the inherent variability of the system, these methods worsened alignment, suggesting that it may be better not to perform alignment in such cases.

Alignment for Comprehensive Two-Dimensional Gas Chromatography with Dual Secondary Columns and Detectors

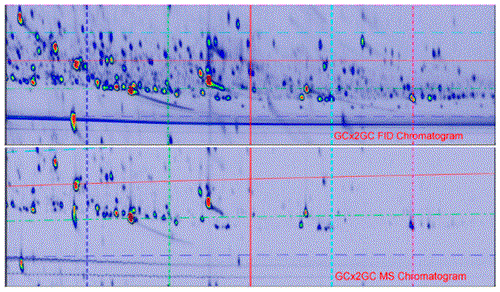
S. Reichenbach, D. Rempe, Q. Tao, D. Bressanello, E. Liberto, C. Bicchi, S. Balducci, and C. Cordero. Analytical Chemistry, 87(19), pp. 10056-10063, 2015.

In each sample run, comprehensive two-dimensional gas chromatography with dual secondary columns and detectors (GC × 2GC) provides complementary information in two chromatograms generated by its two detectors. For example, a flame ionization detector (FID) produces data that is especially effective for quantification and a mass spectrometer (MS) produces data that is especially useful for chemical-structure elucidation and compound identification. The greater information capacity of two detectors is most useful for difficult analyses, such as metabolomics, but using the joint information offered by the two complex two-dimensional chromatograms requires data fusion. In the case that the second columns are equivalent but flow conditions vary (e.g., related to the operative pressure of their different detectors), data fusion can be accomplished by aligning the chromatographic data and/or chromatographic features such as peaks and retention-time windows. Chromatographic alignment requires a mapping from the retention times of one chromatogram to the retention times of the other chromatogram. This paper considers general issues and experimental performance for global two-dimensional mapping functions to align pairs of GC × 2GC chromatograms. Experimental results for GC × 2GC with FID and MS for metabolomic analyses of human urine samples suggest that low-degree polynomial mapping functions out-perform affine transformation (as measured by root-mean-square residuals for matched peaks) and achieve performance near a lower-bound benchmark of inherent variability. Third-degree polynomials slightly out-performed second-degree polynomials in these results, but second-degree polynomials performed nearly as well and may be preferred for parametric and computational simplicity as well as robustness.

PhD Thesis

Advised by Leonidas Guibas

Undergraduate Thesis

Advised by Stephen Scott and Stephen Reichenbach